How To Get Rid Of Ln In An Equation? – Solve Natural Log Expressions

If you are looking for a method on how to get rid of ln in an equation, this article is for you. In this post, you’ll learn the basic rules for natural logarithm (ln) and how to use them to get rid of ln in equations.

How To Get Rid Of Ln In An Equation?

To get rid of ln in an equation or solve the ln (natural log), we can take the inverse function of ln(x) on both sides. In this case, the inverse of ln(x) is the exponential function (e^x). As the function ln and e cancel each other out so, you can get rid of ln in the equation.

Here is a simple example for you: ln(x) = 5

So, to solve this, we add the e^x to both sides: e^ln(x) = e⁵

Because ln and e are inverse functions, they cancel out each other, and then we get: x = e⁵

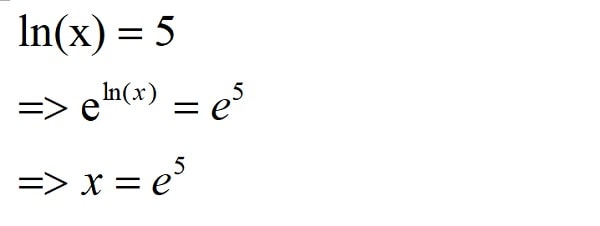
To know how to solve an equation with including ln, we need to understand the definition, the rules, and the inversion functions for ln.

Now, let’s go into details.

What does ln mean in math?

In mathematics, ln is the natural logarithm which is equal to the logarithmic function with base e:
log_e = ln

Thus, the natural logarithm of x is ln (x) = loge (x), where e is a constant approximately equal to 2.718.

What is the inverse of ln(x)?

Because the inverse function of the logarithm is the exponential function with the same base, which is e^x, the inverse of ln(x) is e^x. So here, we have:

• ln(e^x) = x  (x > 0)
• e^ln(x) = x  (x is any real number ℝ)

What are the rules for ln?

The rules for the natural logarithm (ln) are the same as those for the logarithm. Essential rules that need for solving exponential and logarithmic equations include:

• ln (1) = 0
• ln (e) = 1
• ln (ab) = ln (a) + ln (b) (x > 0, y > 0)
• ln (a/b) = ln (a) – ln (b)
• ln aⁿ = n x ln (a) (n > 0)

How do you simplify ln(x)?

By applying the rules for ln, we can know how to simplify or condense the ln that are separated by subtraction or addition. Examples:

• 2 ln 5 – ln 3

For the above example, we will apply the rule ln (a/b) = ln (a) – ln (b). So, we can simplify this equation as follows.

2 ln 5 = ln 5² = ln 25 (applying rule: ln an = n x ln (a) (n > 0)
=> 2 ln 5 – ln 3 = ln 25 – ln 3 = ln (25/3)

• 2 ln x + ln (x+1)

For this example, we will apply the rule ln (ab) = ln (a) + ln (b) (x > 0, y > 0). So, this equation can be simplified as follows.

2 ln x + ln (x+1) = ln x² + ln (x+1) = ln (x^{2 (x+1)})

What Cancels Out Ln?

The function that cancels out natural logs (ln) is the exponential function (e^x) because ln is the inverse function of e^x.

As both of them cancel each other out, they can be applied to solve exponential and natural logarithmic expressions.

How to cancel out ln with e?

To cancel ln expressions with e, we need to take e on both sides of the equations and apply the rules for ln to solve it.

For example, we have an equation with ln as the following: ln 2x – ln 3 = 2

In this example, we need to simplify the ln before canceling it with e. So, using the division rule for ln, we have:

ln 2x – ln 3 = 2
=> ln (2x/3) = 2

Then, take e on both sides of the simplified equation, and we have:

e^{ln (2x/3)} = e²
=> 2x/3 = e² (because e^ln(x) = x, here x = e² >0)
=> x = 2e²/3
=> x = 11

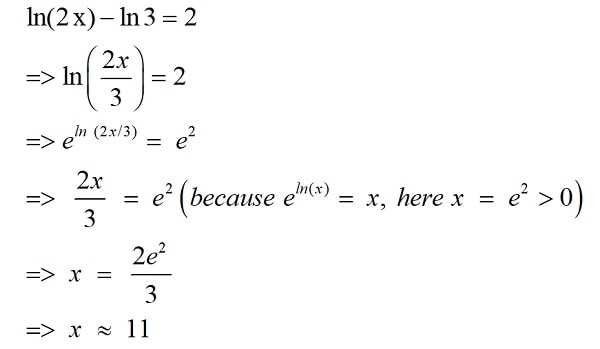
How to cancel out e with ln?

To cancel e with natural logs, we need to add ln on both sides of the equations and use the ln properties to solve the equation.

Let’s take an example and solve it together. 

6e^x + 1 = 3

Before taking ln on both sides of this exponential equation, we need to simplify it to have the equation form of e^x = x. So, in this case, we subtract 1 from and divide 6 by both sides, then we have: e^x = 2/6 = 1/3

Take ln on both sides, and we have:

ln e^x = ln (1/3)
=> x = ln (1/3 ) = -1.099

Is Ln The Same As Log?

Actually, ln is not the same as log because the log is the logarithm with base 10, and ln is the logarithmic function with base e.

ln = log e
=> ln (x) = log e (x)

How do you change ln to log?

Assuming that changing ln to log is converting ln to log, we can apply the following equation:

ln(x) = log(x)/log(e) (e=2.718).

For example, ln (4) = log(4)/log(e) = ​1.386

How to get rid of a log on one side?

We can get rid of a log on one side by converting it to the exponential form with the same base. 

Particularly, if the log equation is a complex one, we need to isolate the log first. Then, we identify the base of the log and subsequently rewrite the equation in the exponential form with the identified base. Let’s take a look at the example below.

log₃(x) = 5

As this equation is the log itself, we don’t need to isolate it. The base is the subscript on the right of “log,” which is 3 in this example. Then, we can rewrite the equation using the exponential form:

log₃(x) = 5
=> 3⁵ = x
=> x = 243

• In the case that the base of the log is not written (log x), the base is identified as 10.

For example, log(4x) + 15 = 18. To solve this equation, we first need to isolate the log by subtracting 8 from both sides. Then, we have: log(4x) = 3. As the base is not written, we take the base as 10, and the exponential form of this log is:
4x = 10³ => x = 10³/4 = 250.

FAQs

Video: Solve Exponential Equations With Natural Logs

References:

• https://en.wikipedia.org/wiki/Natural_logarithm